Seção transversal de uma Taça pitagórica - https://pt.abcdef.wiki/wiki/Pythagorean_cup
Um copo pitagórico parece-se com um copo normal, exceto pelo fato de que a tigela tem uma coluna central, dando-lhe a forma de uma bandeja Bundt . A coluna central da tigela é posicionada diretamente sobre a haste do copo e sobre um orifício na parte inferior da haste. Um pequeno tubo aberto corre deste buraco quase até o topo da coluna central, onde há uma câmara aberta. A câmara é conectada por um segundo tubo ao fundo da coluna central, onde um orifício na coluna expõe o tubo (ao conteúdo) à tigela do copo. Quando o copo está cheio, o líquido sobe pelo segundo tubo até a câmara no topo da coluna central, seguindo o princípio de vasos comunicantes de Pascal . Desde que o nível do líquido não ultrapasse o nível da câmara, o copo funciona normalmente. Se o nível aumentar ainda mais, no entanto, o líquido vazará pela câmara para o primeiro tubo e para fora do fundo. A gravidade então cria um sifão através da coluna central, fazendo com que todo o conteúdo do copo seja esvaziado pelo orifício na parte inferior da haste. A maioria dos banheiros modernos opera com o mesmo princípio: quando o nível da água na tigela aumenta o suficiente, um sifão é criado, esvaziando a tigela.
O copo de Pitágoras é uma demonstração clássica de hidrodinâmica baseada no princípio do sifão. Este instrumento parece apenas uma taça comum, mas quando enchemos a taça todo o líquido se esvai.
Perceba que dentro da taça há um tubo que inicia na parte baixa do reservatório e sobe, para então fazer uma curva e descer até o pé da taça. O copo pode ser usado normalmente, desde que o líquido não alcance a curva do tubo, momento no qual o copo esvazia pelo tubo.
O funcionamento do instrumento é bastante simples. Enquanto enchemos o copo, o líquido vai se acumulando e subindo tanto no reservatório quanto no tubo, pelo princípio de Pascal dos vasos comunicantes. Quando o líquido atinge a curva do tubo, a ação da gravidade sobre o líquido faz com que este seja expelido pelo orifício no fundo do copo.
Este mesmo princípio é utilizado ainda hoje em vasos sanitários e pias, para impedir a passagem de cheiro, e muitos outros equipamentos. Entender funcionamento do sifão é extremamente importante para dominar as tecnologias de hidráulica e transporte de líquidos.
Sobre o funcionamento do sifão
Para entender o funcionamento de um sifão é importante estudar um pouco sobre hidrodinâmica, mais especificamente o princípio (ou teorema) de Bernoulli. Este princípio descreve o comportamento de um fluido em movimento e pode ser deduzido a partir da conservação de duas grandezas: massa e energia.
Considerando um fluido incompressível e sem atrito, o seu movimento é descrito pela equação de Bernoulli, dada por: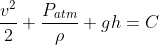 
, onde 
é a velocidade de escoamento do fluido, 
é a pressão atmosférica,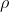 
é a densidade do fluido, 
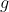é a aceleração da gravidade, 
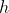é a altura da coluna de líquido e 
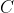uma constante. O primeiro termo da equação se refere à energia cinética, o segundo à pressão e o terceiro à energia podencial gravitacional.
Aplicando esta equação para um sifão podemos considerar uma linha de fluxo que parte da superfície do reservatório e vai até o orifício no final do sifão. Para esta linha de fluxo, o valor 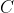é constante e podemos igualar as equações nos diversos pontos de interesse e obter os valores de velocidade para o escoamento, assim como observar os limites para os quais o escoamento acontece.
demonstra que a velocidade de escoamento depende apenas da aceleração da gravidade e da diferença de altura entre o nível do reservatório e a saída do tubo do sifão.
mostra que a velocidade máxima de escoamento depende da pressão atmosférica, da densidade do líquido, da aceleração da gravidade e da diferença de altura entre o nível do reservatório e o ponto mais alto do tubo do sifão.
A profundidade da entrada do tubo do sifão não faz diferença para os resultados da dinâmica. É claro que isso só se aplica no caso ideal em que estamos tratando, mas é uma boa aproximação para o que acontece na realidade.
Brincando com as equações e considerando a aproximação de que o reservatório seja muito grande, obtemos os seguintes resultados interessantes:
ufrgs.br
wiki.pt
Sem comentários:
Enviar um comentário